このページの結論を先に言うと、
- スタックは、最後に入れたデータを最初に取り出すデータ構造
- キューは、最初に入れたデータを最初に取り出す構造
- 木構造は、データが辺でつながっていて、閉路のないもの
- 木構造のデータ探索には、キューを使うと幅優先探索、スタックを使うと深さ優先探索
以下で詳しくやります。
スタック
スタックは「Last-In, First-Out」、つまり最後に入れたデータを最初に取り出すデータ構造です。
イメージとしては、本をひとつずつ山積みにしていき、使うときは一番上の本を取り出すことに似ています。

Pythonでスタックを扱うには、リストに対して「append」と「pop」メソッドを使います。
$ python3
Python 3.10.0 (default, Oct 12 2021, 16:02:08) [GCC 9.3.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> stack = []
>>> stack.append('a')
>>> stack.append('b')
>>> stack.append('c')
>>> stack.append('d')
>>> stack
['a', 'b', 'c', 'd']
>>> stack.pop()
'd'
>>> stack.pop()
'c'
>>> stack.pop()
'b'
>>> stack.pop()
'a'
キュー
キューは「First-In, First-Out」、最初に入れたデータを最初に取り出すデータ構造です。
イメージとしては、レジや窓口などの行列に例えることができます。
最初に処理されるのは先頭の人です。

Pythonでキューとして扱うには、スタックと同じようにリストを使って「append」と「pop(0)」でも可能ですが、メモリ効率や速度などのパフォーマンスを考えると、「collections」モジュールの「deque」クラスを使う方が良さそうです。
>>> from collections import deque
>>> abc = ['a', 'b', 'c']
>>> que = deque(abc)
>>> que.append('d')
>>> que.append('e')
>>> que
>>> deque(['a', 'b', 'c', 'd', 'e'])
>>> que.popleft()
'a'
>>> que.popleft()
'b'
>>> que
deque(['c', 'd', 'e'])
dequeにリストを渡して初期化し、追加には「append」、取り出しには「popleft」を用いています。
dequeクラスはスタックとしても扱えます。
>>> stack = deque() >>> stack deque([]) >>> stack.append(1) >>> stack.append(2) >>> stack.append(3) >>> stack deque([1, 2, 3]) >>> stack.pop() 3 >>> stack.pop() 2 >>> stack.pop() 1
Pythonにはdequeの他に「queue」というライブラリもありますが、こちらはマルチスレッドプログラミングの際に有益なようです。
速度に関して、リスト・queue・dequeで計測して比較している方がいたので、以下の記事を参照してください。
[Qiita]Pythonのスタックとキューには何を使えばいいのか
「deque」が良さそうですね。
木構造
データが辺でつながっていて、閉路を持たないものを木構造と言います。
木の中で特定データをスタート地点としたものが根付き木です。
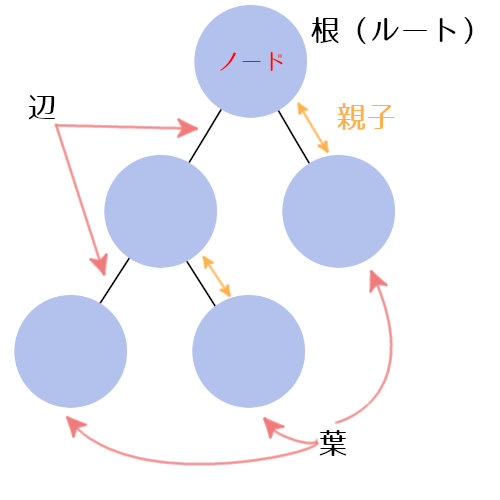
データのひとつひとつをノードと言い、なにかしらの値を持ちます。
大本になっているノードが根です。
ノードは辺でつながっていて、各ノードから見たとき上につながっているものが「親」、下につながっているものが「子」の関係になります。
もし辺が△のようにつながっていて閉路があった場合は、木ではなくグラフになります。
子を持たない末端のノードが葉です。
二分木の種類
ノードの子の数が2つ以下のものを二分木(Binary-Tree)と言います。
子が3つ以上持つものは多分木。
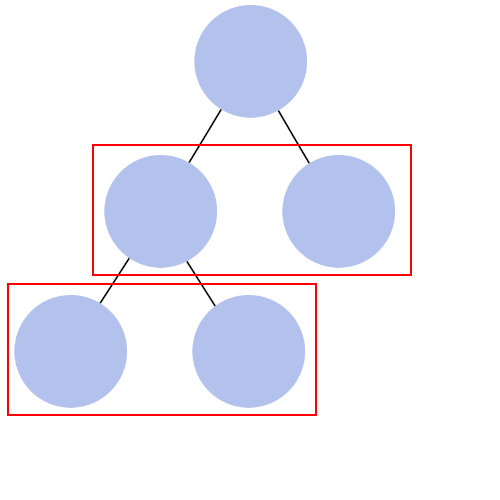
二分木は、さらに種類分けができます。
- 完全二分木
- 葉のすべてが同じ深さ(横一列並び)であり、子が2つ(あるいは2つずつ)であるもの
- 二分探索木
- 親ノードから見て、左と右に子ノードがつながっているとき、左の子ノードの値は親ノードの値以下、右の子ノードの値は親ノード以上になっているもの
- 平衡二分探索木
- 二分探索木のなかで葉がなるべく同じ深さになるようにしたもの
- 二分ヒープ
- 親ノードの値が常に子ノードの値よりも大きく(または小さく)なるように配置したもの
二分木の実装
二分木を簡単なクラスを使って実装しました。
class Node():
def __init__(self, data):
self.data = data
self.left = None
self.right = None
root = Node(0)
root.left = Node(1)
root.right = Node(2)
root.left.left = Node(3)
root.left.right = Node(4)
root.right.left = Node(5)
root.right.right = Node(6)
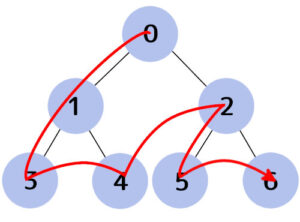
上記の木構造を図にすると次のようになります。
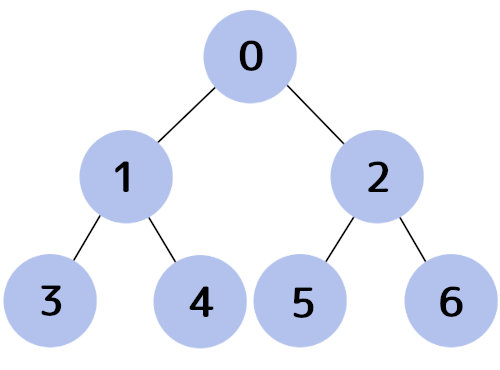
幅優先探索と深さ優先探索
木のデータ探索方法は2つです。
幅優先探索(Breadth-first search)――ルートから近いノードを順に探索する方法。
深さ優先探索(Depth-first search)――ルートから奥へ向かっていき、行けるところから順に探索する方法。
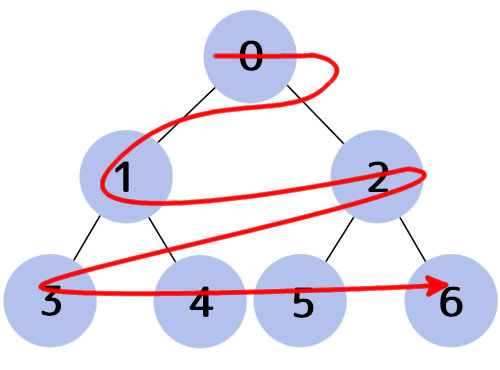
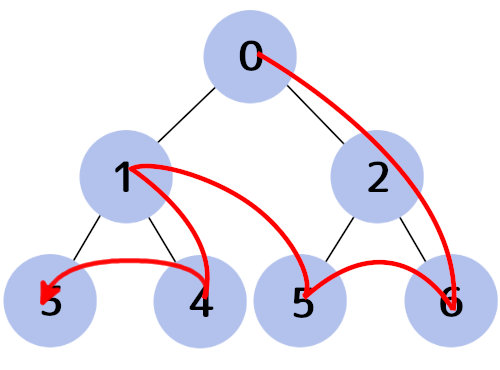
幅優先探索はキューを、深さ優先探索はスタックを使うと実現できます。
以下は幅優先探索を使ったコードです。
キューをスタックに変更すると深さ優先探索になります。
from collections import deque
class Node():
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# 幅優先探索で出力
def bfsearch(root):
que = deque([root])
while que:
node = que.popleft()
print(node.data, end=' ')
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
print()
root = Node(0)
root.left = Node(1)
root.right = Node(2)
root.left.left = Node(3)
root.left.right = Node(4)
root.right.left = Node(5)
root.right.right = Node(6)
bfsearch(root)
whileの各回転が終わったときの各変数の中身は次のようになります。
| ループ回数 | node変数 | que変数 |
|---|---|---|
| 1 | root | [root.left, root.right] |
| 2 | root.left | [root.right, root.left.left, root.left.right] |
| 3 | root.right | [root.left.left, root.left.right, root.right.left, root.right.right] |
| 4 | root.left.left | [root.left.right, root.right.left, root.right.right] |
| 5 | root.left.right | [root.right.left, root.right.right] |
| 6 | root.right.left | [root.right.right] |
| 7 | root.right.right | [] |
ループの4回目以降は「if」文が偽になるで、新たにキューに追加されることがありません。
スクリプトを実行すると意図通りの出力になりました。
$ python3 bfsearch.py 0 1 2 3 4 5 6
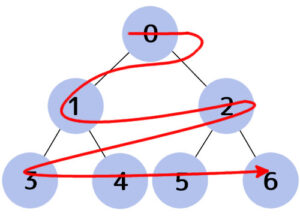
以上キューを使った幅優先探索でした。
深さ優先探索もやっておきます。
def dfsearch(root):
stack = deque([root])
datas = []
while stack:
node = stack.pop()
datas.append(node.data)
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
for i in datas:
print(i, end=' ')
print()# 出力 0 2 6 5 1 4 3
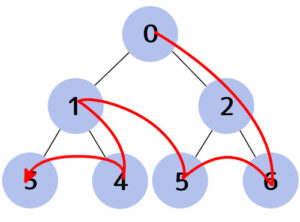
関数名と、dequeクラスを入れる変数名を変え、popメソッドを使うようにしただけです。
深さ優先探索は再帰を使ってもできます。
def recursion(node):
if node:
print(node.data, end=' ')
recursion(node.left)
recursion(node.right)
# 出力 0 1 3 4 2 5 6
すっきりと簡潔に書けました。
出力はスタックを使った方法とは逆側からになっていますが、recursion(node.left)とrecursion(node.right)を入れ替えると同じ結果が得られます。